Navigating the Road: The Importance of Lines in Ensuring Order and Safety

Lines: The Unsung Heroes of Order and Guidance on Our Roads

When we think about the elements that contribute to road safety, we often overlook one crucial aspect – lines. These seemingly simple markings play a vital role in guiding and organizing traffic, ensuring a smooth and safe flow of vehicles on our roads. From the familiar white and yellow lines to specialized markings, lines are the unsung heroes that keep our roads orderly and efficient.

One of the most common types of road markings is the white line. These lines act as dividers, separating lanes for different directions of traffic. They provide clear boundaries, preventing vehicles from drifting into oncoming traffic or straying out of their designated lanes. White lines also indicate where overtaking is allowed or prohibited, helping drivers make informed decisions while navigating busy roads.

Yellow lines, on the other hand, serve a different purpose. Found primarily in urban areas, they indicate parking restrictions and help manage traffic flow. Single yellow lines typically mean limited parking during certain hours, while double yellow lines signify no parking at any time. By clearly marking these restrictions, yellow lines ensure that traffic can move smoothly without unnecessary obstructions.

Specialized markings further enhance road safety by addressing specific needs. For instance, cycle lanes are marked with distinctive symbols and colors to designate dedicated space for cyclists. These markings not only protect cyclists but also raise awareness among drivers to be mindful of sharing the road with vulnerable road users.

Pedestrian crossings are another example of specialized markings that prioritize pedestrian safety. Zebra crossings with bold black and white stripes provide a clear indication for drivers to yield to pedestrians who wish to cross the road safely. Such markings contribute significantly to reducing accidents involving pedestrians by creating awareness and encouraging responsible driving behavior.

In addition to guiding traffic flow, road markings also help regulate speed limits. Speed limit signs are often accompanied by painted speed limit roundels on the road surface itself. These roundels act as visual reminders for drivers, reinforcing the speed limit and promoting compliance.

While road markings are essential for road safety, they are not immune to wear and tear. Harsh weather conditions, heavy traffic, and regular maintenance activities can cause lines to fade or become less visible over time. To ensure their effectiveness, regular maintenance and repainting of road markings are necessary.

In conclusion, lines may seem like simple markings on our roads, but they play a crucial role in maintaining order and guiding traffic. From separating lanes to indicating parking restrictions and protecting vulnerable road users, lines contribute significantly to road safety. It is important that we recognize their importance and appreciate the efforts made by professionals who diligently maintain these markings for our benefit. So next time you’re on the road, take a moment to acknowledge the unsung heroes – the lines that keep us safe and organized.

Commonly Asked Questions About Lines in Geometry

What is the meaning of a straight line?
How do you draw a straight line?
What is an angle in geometry?
How do you calculate the slope of a line?
What are the different types of lines in geometry?
How can I find the equation of a line given two points?

What is the meaning of a straight line?

A straight line is a geometric concept that represents the shortest distance between two points. It is a perfectly linear and uninterrupted path that extends infinitely in both directions. In mathematics, a straight line is often represented by the equation y = mx + c, where m is the slope (gradient) of the line and c is the y-intercept (the point where the line intersects the y-axis). A straight line has no curves, bends, or angles, making it the simplest form of a geometric shape. Its simplicity and predictability make it a fundamental element in various fields such as mathematics, physics, engineering, and design.

How do you draw a straight line?

Drawing a straight line may seem like a simple task, but it can require some practice and technique to achieve a perfectly straight result. Here are a few methods you can try:

Freehand: To draw a straight line freehand, position your pen or pencil on the paper where you want the line to begin. Keep your hand steady and use your wrist or arm to guide the pen or pencil along the desired path. Focus on maintaining a consistent pressure and speed as you move across the paper.
Ruler or Straightedge: Using a ruler or straightedge is one of the most reliable ways to draw a straight line. Place the ruler or straightedge on the paper where you want the line to be drawn. Hold it firmly in place with one hand while using your other hand to draw along its edge with a pen or pencil. The ruler will act as a guide, ensuring that your line remains perfectly straight.
Taut String: If you don’t have access to a ruler or straightedge, another method is using a taut string as a makeshift guide. Attach one end of the string to an anchor point (such as tape) at one end of where you want your line to be drawn. Hold the other end of the string tightly and use it as a guide for drawing your line by pulling it taut and tracing along its length.
Mechanical Drawing Tools: For more precise and technical drawings, mechanical drawing tools like compasses, protractors, and T-squares can be used to create accurate straight lines and angles.

Remember that practice makes perfect when it comes to drawing straight lines. It’s also important to choose appropriate materials such as pens or pencils with sharp points for better control and accuracy.

What is an angle in geometry?

In geometry, an angle is a fundamental concept that describes the relationship between two intersecting lines or line segments. It is formed by two rays or line segments that share a common endpoint, known as the vertex of the angle.

Angles are typically measured in degrees (°) or radians (rad). A full circle is divided into 360 degrees or 2π radians. Angles can be classified based on their measure:

Acute Angle: An acute angle measures less than 90 degrees (or less than π/2 radians).

Right Angle: A right angle measures exactly 90 degrees (or π/2 radians). It forms a square corner and is denoted by a small square in the vertex.

Obtuse Angle: An obtuse angle measures more than 90 degrees (or more than π/2 radians) but less than 180 degrees (or π radians).

Straight Angle: A straight angle measures exactly 180 degrees (or π radians). It forms a straight line and is denoted by a small line segment in the vertex.

Reflex Angle: A reflex angle measures more than 180 degrees (or π radians) but less than 360 degrees (or 2π radians).

Angles can also be classified based on their relationship to other angles:

Complementary Angles: Two angles are complementary if their sum equals exactly 90 degrees (or π/2 radians).

Supplementary Angles: Two angles are supplementary if their sum equals exactly 180 degrees (or π radians).

Adjacent Angles: Two angles are adjacent if they have a common vertex and share a common side between them.

Understanding angles is essential in various mathematical disciplines, including geometry, trigonometry, and physics. They help us describe and analyze shapes, determine distances and measurements, and solve complex problems involving spatial relationships.

Remember, when working with angles, it is important to use appropriate units of measurement and consider the specific properties and relationships associated with each type of angle.

How do you calculate the slope of a line?

To calculate the slope of a line, you need to know the coordinates of two points on that line. Let’s call these points (x1, y1) and (x2, y2). The slope, often denoted as “m,” represents the ratio of the vertical change (y2 – y1) to the horizontal change (x2 – x1) between these two points.

The formula for calculating slope is:

m = (y2 – y1) / (x2 – x1)

For example, let’s say we have two points on a line: Point A with coordinates (3, 5) and Point B with coordinates (7, 9). To find the slope between these two points:

m = (9 – 5) / (7 – 3)

= 4 / 4

= 1

In this case, the slope of the line is 1. This means that for every unit increase in the horizontal direction (x), there is an equal increase of one unit in the vertical direction (y).

It’s worth noting that if the line is vertical and parallel to the y-axis, the slope is considered undefined because there is no change in x. Similarly, if two points have identical x-coordinates, there is no horizontal change and dividing by zero would make the slope undefined as well.

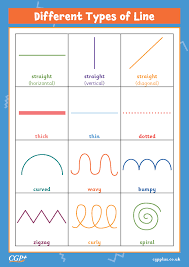
What are the different types of lines in geometry?

In geometry, lines are fundamental elements that help define shapes and relationships between points and other geometric objects. Here are some of the different types of lines commonly studied in geometry:

Straight Line: A straight line is the most basic type of line. It extends infinitely in both directions and has no curves or bends.
Parallel Lines: Parallel lines are two or more lines that never intersect, no matter how far they are extended. They always remain equidistant from each other.
Perpendicular Lines: Perpendicular lines are two lines that intersect at a right angle (90 degrees). The point of intersection is known as the “point of perpendicularity.”
Intersecting Lines: Intersecting lines are two or more lines that meet or cross at a single point.
Transversal Line: A transversal line is a line that intersects two or more other lines at distinct points.
Diagonal Line: A diagonal line connects non-adjacent vertices in polygons, such as squares or rectangles.
Horizontal Line: A horizontal line is parallel to the horizon and has a slope of zero (0). It extends left and right but does not go up or down.
Vertical Line: A vertical line is perpendicular to the horizon and has an undefined slope. It extends up and down but does not go left or right.
Ray: A ray is a part of a line with one endpoint that extends infinitely in one direction.
Line Segment: A line segment is a part of a line with two endpoints, representing a finite length between those points.

These different types of lines serve as building blocks for various geometric concepts and calculations, allowing mathematicians to study shapes, angles, distances, and much more within the field of geometry.

How can I find the equation of a line given two points?

To find the equation of a line given two points, you can use the slope-intercept form of a linear equation: y = mx + b. Here are the steps:

Identify the coordinates of the two points on the line. Let’s call them (x1, y1) and (x2, y2).

Calculate the slope (m) using the formula: m = (y2 – y1) / (x2 – x1). The slope represents how steep or flat the line is.

Once you have the slope, you can substitute it into the slope-intercept form equation along with one of the points to find the y-intercept (b). Choose either (x1, y1) or (x2, y2).

Using (x1, y1):

y = mx + b

Substitute x = x1 and y = y1:

y1 = m(x1) + b

Solve for b:

b = y1 – m(x1)

Now that you have both the slope (m) and the y-intercept (b), you can write down the equation of your line in slope-intercept form: y = mx + b.

Remember to substitute in your specific values for m and b based on your calculations. This equation will represent a straight line that passes through both given points.